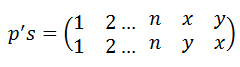Length Contraction

Lorentz Length Contraction

(The mathematics of this proof requires the equations that we came up with in the proof of time dilation.)

If we take a an object with a length L₀  and move it with a constant velocity 'v' to the right, the object will have a length of L'.

Under Newtonian mechanics (where there would be no time dilation) we can express the x and x' values like this:

However, due to relativity, we must take into account the relativistic time dilation with velocity. This gives us:

 The x values can be used to express L₀ , and the x' values can be used to express the L' values:

 We can then substitute the relativistic values of x1 and x2 into the equation of L₀ :

 

Substituting L' for the numerator gives:

Which can be re-arranged to give:

 

 Therefore, velocity has the effect of contracting the length of a body perpendicular to the direction of motionrelative to the observer.

QED

 

So if the rest frame were a 3m long spaceship, and it were to blast off at 0.8c relative to an observer it would appear to have the length of 1.8m. As with time dilation, this effect is only noticeable at velocities a sizeable fraction of light-speed.

 

Time Dilation

Lorentz Time Dilation

This one was requested by a reader, and I think that it's a neat proof of a fundamental property of nature anyway. The only two principles we need to begin with are the principle of relativity - that you can't determine who is at rest if two people are moving at a constant velocity with respect to one another - and the principle of the equivalence of the speed of light - that light travels at the same speed for everybody (no matter what velocity they are moving at)

We can prove this using a thought experiment and a little bit of algebra. Our thought experiment will require a light clock which works by having two mirrors a set distance apart and bouncing light between them. 

The light clock on the left is stationary to the observer, and the mirrors are a distance L apart. The light clock on the right is in constant motion to the observer with a velocity of v. The distance D is the distance the light travels from the bottom mirror to the top mirror. vt'/2 is the horizontal distance between the points where the light bounces off one of the mirrors in the light clock. Time in the left light clock is represented by t; time in the other light clock is represented by t'.

From the experiment, we can say:

t=2L/c

D=ct'

Using Pythagoras' Theorem and the diagram, we can say:

As we now have two values of D, we can say:

Sqaure each side and re-arrange:

Factorise:

Solve for the square of t':

Take the square root:

Substitute in t from the first formula from the thought experiment:

Thus we can say that at high velocities, time is dilated by a function of the velocity (usually represented by a lower-case gamma: γ)

QED

 

At low, everyday speeds the effect is very small. If we substitue v=0.0001c (0.01% of light speed), then t' will equal 1.0000005000000375 times t, which is only a small dilation of time.

However, at high speeds reached by high-energy particles, the effect can be very noticeable. If we substitute v=0.99c (99% of light speed), the t' will equal 7.0888120501 times t. Which means that if someone were moving at 99% the speed of light with repect to an observer, the observer will pass through time 7 times faster than the person in motion.

It is because we don't experience these kinds of velocities in our everyday lives that it took us so long to discover the effects of time-dilation.

The Futurama Theorem

The Futurama Theorem:

I'm afraid we need to use math(s)!

Hypothesis: 

Bad news everybody...

Professor Farnsworth created a machine that allows the switching of the minds of two people. However, the switch can only occur between two people once only. There have been multiple switches between characters in the episode. 

There needs to be a maximum of two people who haven't previously used the machine in order to restore the original minds and bodies.

Proof:

(For those acquainted with group theory)

 First, let p be some K-cycle on [n] = {1…n}

Let (a,b) represent the transposition that switches the contents of a and b.

 Introduce two "new bodies" x and y to give p'

For any i = 1 to k, let s be the left to right series of switches

By verification: p's inverts the K-cycle and leaves x and y switched without performing the transposition (x,y)

 

By allowing p to be a perrmuation on [n], the sequence above shows the method of inversion. x and y can be switched manually after by (x,y) if need be.

QED

(In plain English)

1. Have everybody arrange themselves in circles, each facing their mind's original body
2. Get two new people (X and Y)
3. Fix the circles one by one
• Start each time with X and Y having their minds in their own body
• Unwrap any circle of people into a line 
• Swap the mind at the front into person X's body
• From the back of the line, have everybody swap with person Y in turn.
• Swap the mind in person X's body to the person at the back of the line
4. Swap the minds in the bodies of person X and person Y if need be

Hooray for Zoidberg!

The Bohr Model: The Basics

• 

  A Bohr Model Diagram

  The Bohr model shows that the electrons in atoms are in orbits of differing energy around the nucleus (think of planets orbiting around the sun).
• Bohr used the term energy levels (or shells) to describe these orbits of differing energy. He said that the energy of an electron is quantized, meaning electrons can have one energy level or another but nothing in between.
• The energy level an electron normally occupies is called its ground state. But it can move to a higher-energy, less-stable level, or shell, by absorbing energy. This higher-energy, less-stable state is called the electron’s excited state.
• After it’s done being excited, the electron can return to its original ground state by releasing the energy it has absorbed, as shown in the diagram below.
• Sometimes the energy released by electrons occupies the portion of the electromagnetic spectrum (the range of wavelengths of energy) that humans detect as visible light. Slight variations in the amount of the energy are seen as light of different colors.

Spectral Lines

Emission Spectrum of Hydrogen

The emission spectrum of hydrogen

From experiment, the wavelengths of light emitted from a hydrogen atom are: 410nm, 434nm, 486nm, and 656nm.

The only equtions we need to know for this are E=hf (Planck's formula), and c=λf. From this, we can say that the energy of a photon (a particle of light) can be given by E=hc/λ. We can use this to calculate the energies that the photons emitted by the hydrogen atom are. Then, we will develop the mathematics behind the Bohr model and test our theory with this experimental data.

From the previous proof of the Bohr radius,  we said that the energy of an electron orbiting a nucleus in a hydrogen atom was given by the equation: E = Ar^-2 – Br^-1, and we found that r was given by the equation: r=2A/B. (A and B were arbitrary constants that we will substitute in later.)

If we substitute r=2A/B into the equation E = Ar^-2 – Br^-1, and substitute in the values for constants A and B we get the following formula.

n is the energy shell that the electron occupies and all of the other numbers are constants independant of thre state of the electron. So the formula can be expressed as:

We can assign another constant, x, to make our calculations slightly easier:

 So, now we can express an electron in an energy level n by the formula: E= -x/n², so the change in energycan be represented by the following equation:

 In order to conserve energy, the energy lossed by the electron will also be the same as the energy of the light released. So the energies of light that we got from the experimental data at the start of the proof needs to fit the formula we just made. 

 If the electron goes from the sixth energy level to the second energy level, we can find out the chnage in energy by substituting 6 for n1 and 2 for n2. Similarly, we can do this for any energy jump in the hydrogen atom. The visible photon energies from the experimental data correspond to the following electron jumps: n=6 to n=2, n=5 to n=2, n=4 to n=2, and n=5 to n=2.

Therefore, the visible emission spectrum of a hydrogen atom is due to the electron in the hydrogen atom moving between specific energy levels.

QED