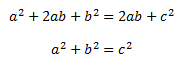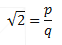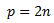Hubble's Law

Hubble's Law

Using Pogson's Law and the Doppler Effect, we can make the biggest and most profound statement in Cosmology.

Pogson's Law can determine the distance a galaxy is from Earth, and the Doppler Effect can determine the galactic radial velocity relative to Earth. Plotting the radial distance against radial velocity on a graph gives an interesting result.

Remarkable...

. 
The line of best fit on the graph is a straight line which implies that the recessional velocity is directly proportional to the distance of the galaxy. This is also known as Hubble's Law.

Since Vr is conventionally expressed in units of km/s and r in units of Mpc, the units of the constant (Hubble's Constant) are km.s(^-1)/Mpc.

From the graph, we can see that the furthest galaxies are moving away from us at a faster rate than closer galaxies. This is what would be expected if all galaxies were to move away from one another from a single point as if from a big explosion - commonly known as 'the Big Bang'.

Hubble's Constant also gives us some information about how much time has elapsed since the Big Bang event. As H=V/r, by assuming that each galaxy has traveled a distance of r at constant velocity V in time T we can show that V=r/T. Hence, T=1/H.

By cancelling the units of Hubble's Constant to 1/s, the reciprocal of that value is the age of the universe in seconds. The agreed value of the age of the Universe is 4.3×10¹⁷ seconds, which is equivalent to around 13.8 billion years.

The fact that mankind can determine the age of the universe so easily still amazes me...

Remarkable...

Doppler Effect

The Doppler Effect

The Doppler effect causes waves, such as sound and light to change wavelength depending on the velocity of the observer in relation to the velocity of the emitter of the wave.

 

Nnnyyyooowww

The Doppler effect is expressed with the relation: Δλ/λ(rest) = v/c

v is the radial velocity of the emitter when the observer perceives themselves to be at rest.
λ(rest) is the wavelength of light (or sound) that would be observed from the object if it were at rest relative to the observer.
  Δλ is the difference between the observed wavelength and λ(rest).
c is the speed of light.

In stars with similar surface temperatures as the Sun, the spectral absorption of ionised calcium feature prominent H and K lines. These lines can be studied in an Earth-bound laboratory quite easily to determine the value of λ(rest). The K line has a λ(rest) of 393.37nm and the H line has a λ(rest) of 396.85nm.

Because these lines are easily observable in distant galaxies, a spectrometer can be used to determine the value for λ for both lines. Due to the Doppler Effect, the values for λ and λ(rest) for each line will differ by the same Δλ. Using the equation Δλ/λ(rest) = v/c, the radial velocity of the galaxy can be experimentally determined.

Deriving the Schrodinger Equation

The Schrodinger Equation

The Schrodinger equation was formulated in 1925 and is used to describe how the state of a quantum mechanical system changes with time. The equation can be formulated with knowledge of differential calculus and of the quantum action principle.

The quantum action principle gives the following identity to a wavefunction of a free particle (Eq. 1):

Each point in spacetime has a wavefunction corresponding to a certain particle, and initially we will confine it to two dimensions: x and t.

Differentiating the wavefunction with respect to time yields a term for total energy (for a free particle, or when there is no potential energy on the particle), (Eq. 2):

Taking the second differential of the wavefunction with respect to space (in this case, just the x-dimension) yields a term for kinetic energy (Eq. 3):

It is assumed that energy is conserved, and a Hamiltonian from classical mechanics is used (the Hamiltonian is the sum of the kinetic and potential energy). It is also assumed that the potential does not vary with time, but it varies with space (which is why Eq. 2 resulted in the total energy, and Eq. 3 resulted in the kinetic energy).

The Hamiltonian is represented by Eq. 4:

Substituting the values of E and K from Eq. 2 and Eq. 3 respectively into Eq. 4 yields Eq. 5:

This can then be placed into the four dimensions of spacetime by using the del operator,  using a distance 'r' to show the spatial distance from a fixed point in the system, and allowing the potential energy of to change with time yields Eq. 6:

 

This shows that the equation for the wavefunction as shown in Eq.1 is valid for a non-relativistic, free, spinless particle as it has been shown to be equivalent to the Schrodinger equation (which deals with non-relativistic, spinless wavefunctions) when applied to the principle of conservation of energy.

QED

(Equation 1 adapted from 'The Quantum Universe: Anything That Can Happen Does Happen', Cox & Forshaw) - Recommended Read!

Pogson's Law

Pogson's Law

This post is one in three of a series on Astronomy. It determines the distances of galaxies by looking at their magnitude

Magnitude

Stellar brightness is based on a convention first devised by Hipparchus. The brightest stars that can be seen with the eye have a magnitude of 1.0; the faintest have a magnitude of 6.0. Due to the invention of the telescope, stars with negative apparent magnitudes can be seen. It is important for us to note that the more negative the apparent magnitude, the brighter a star appears.

This is for the following reason: the human eye perceives equal ratios of brightness at equal intervals. This means the difference in brightness of a 100W light bulb to a 200W light bulb would appear the same as the difference.

On the original scale, the flux (W/m^2) from stars of the first magnitude was about 100 times greater than that from stars of the sixth magnitude. Thus a difference of 5 magnitudes gives a flux ratio of 100. A magnitude difference of 1 would therefore correspond to a flux ratio of (100)^(1/5) = 2.512.

This can be re-formulated (as was by Pogson) into the mathematical definition: 

m(1) - m(2) = -2.5 log [f(2)/f(1)]

Where: m(1) and f(1), and m(2) and f(2) are the apparent magnitudes and fluxes of star 1 and star 2, respectively.

To estimate stellar and galactic distances, an absolute scale must be established. This can be done by looking at the consequences of having all stars equidistant from Earth, meaning the difference in stellar and galactic luminosity would be the only factor affecting the luminosity. The absolute magnitude, M, is therefore the apparent magnitude a star or galaxy as if it were 10 parsecs from Earth.

Assuming that the light is spread evenly by the star or galaxy in question, then the flux can be determined by the equation: f(10) = L/4(pi)(r^2), where r is 10 parsecs, and f(10) is the flux a star would have at that distance, and L is the luminosity of the star.

Thus: m-M = -2.5 log [f/f(10)], and f/f(10) = ((10^2)/(r^2)) = (10/r)^2

We can now re-write Pogson's law as: m-M = -2.5 log[(10/r)^2]
= -5 log(10) + 5 log r

Thus: m - M = 5 log r - 5

Which can be re-arranged to: r = 10^[(m+27)/5]

QED

Therefore, we can use the apparent magnitude of distant stars to show their distance from Earth in parsecs. For example, the galaxy coma2 has the apparent magnitude of 12.55 and thus is 81.28 Mega-parsecs from Earth.

Platonic Solids

Platonic Solids

This one is because I'm on a roll with geometry. (See escape velocity)

This post will prove that there are a limited number of regular three-dimensional solids and will determine the nature of these solids.

Euler said that a regular solid obeys the following rule (where V is the number of vertices, E is the number of edges, and F is the number of faces).

This can be expressed using E only by applying a little logic:

Every edge of a regular solid is shared by the sides of 2 adjacent polygons.

Every edge connects two vertices.

Therefore:

(where n is the number of sides each polygon has, and r is the number of polygons that meet at each vertex)

We can divide the new equation by 2E and rearrange to give:

n must be greater or equal to 3 as the simplest polygon is the triangle, and r must be greater than or equal to 3 as at least 3 vertices must meet in a polyhedron.

If both n and r were simultaneously greater than 3, the left hand side of the equation would be less than 2/3 and could not be satisfied if E is a positive integer (which it must be).

If n=3, the equation becomes:

This can give positive integer values of E for when r = 3, 4, and 5.

 If r=3, the equation becomes:

If n=3, we get E=6 again.

In both cases, n and r cannot be greater than or equal to 6. Because n and r must be between 3 and 6, and either n or r must be three for all solids, there is a limited number of valid combinations of n and r. There are only five of these combinations and thus there are only five regular solids.

We will now analyse these results to see what deescribes which solid. To describe the shape we wil use curly brackets to show {n, r}. From earlier we also know that: V=2E/r and F=2E/n, these will be used to determine the nature of these solids.

{3, 3}

When n=3 and r=3, then E=6. Thus V=4 and F=4. Thus we can deduce the following:
The solid consists of four regular triangles, three triangles meet at each of the four vertices forming six edges. This shape is therefore the tetrahedron.

{3, 4}

When n=3 and r=4, then E=12. Thus V=6 and F=8. Thus we can deduce the following:
The solid consists of eight regular triangles, four triangles meet at each of the six vertices forming twelve edges. This shape is therefore the octahedron.

{3, 5}

When n=3 and r=5, then E=20. Thus V=12 and F=20. Thus we can deduce the following:
The solid consists of twenty regular triangles, five triangles meet at each of the twelve vertices forming twenty edges. This shape is therefore the icosahedron.

{4, 3}

When n=4 and r=3, then E=12. Thus V=8 and F=6. Thus we can deduce the following:
The solid consists of four squares, three squares meet at each of the eight vertices forming twelve edges. This shape is therefore the cube.

{5, 3}

When n=5 and r=3, then E=30. Thus V=20 and F=12. Thus we can deduce the following:

The solid consists of twelve regular pentagons, three pentagons meet at each of the twenty vertices forming thirty edges. This shape is therefore the dodecahedron.

Thus, the tetrahedron, octahedron, icosahedron, cube, and the dodecahedron are the only five regular solids.

QED 

These solids were used in Kepler's first attempt at describing at describing a heliocentric model. It worked because the number of known planets at the time was five, and it seemed too much of a coincidence to Kepler. Unfortunately, it was; however, he still went on to discover his three laws of planetary motion.

Aristotle also believed that these solids corresponded to air, earth, fire, water. Apparantly, ordinary people were to be kept ignorant of the dodecahadron - which was not assosiated with an element. However, some philosophers at the time believed in an aether in which the planets moved, and some applied the starry appearance of the dodecahedron to the starry appearance of the night sky.

Escape Velocity

Earth's Escape Velocity

The escape velocity is the velocity required to send a body into orbit around another body, such as a planet. The escape velocity of Earth can be found by using geometry.

There is no escape...

To calculate the velocity, we need to know two numbers: the radius of the body you want to escape from, and the distance an escaping body will fall in one second. In the case of Earth, the radius is 6,380km and the distance fallen in one second in half of the figure for accelaration due to gravity, so we will call it g/2 for now.

Therefore we can say:

R = 6380000m

S = g/2

We can show the Earth as a two dimensional circle like this:

We can use a theorem of plane geometry to help us in our calculation. The tangient to a circle is the mena proportion between two parts of the diametre cut by an equal chord...

...and in algebra speak we get this which can be easily solved for x:

Remember: S = g/2

We can just plug in the values of the radius and for g (9.81ms^-2) to get 7900km if we are using 3 sig. fig.

Thus, as x is the distance we need to send our rocket ship in one second, we can divide by this one second to get a velocity. Thus:

For our friends in Europe.

For those using old money.

Thus, in order to escape the gravitational pull of the Earth and go into orbit, we will have to travel with a velocity close to 8 kilometres (5 miles) a second.

QED

Geometrical diagram made with Geogebra.

Pythagoras and Irrationality

Pythagoras' Theorem

If we have a square with a tilted, smaller square inside (see diagram above), then we can come up with two expressions for the area of the larger square. The first squares the sum of lengths a and b; the second squares the length c, then adds the area of the smaller triangles surrounding the smaller, inner square.

Then we can solve these equations simulataneously for the square of c

Thus we have proved the sum of the squares of the two smallest sides in a right angled triangle is equal to the square of the hypotenuse 

QED

The Square Root of 2 

Pythagorean philsophy believed that everything in the universe could be expressed as the ratio of two integers. These ratios are known as rational numbers and can be also expressed as a non-recurring decimal. for example 10:5 is the same as 2.0. Also, these ratios must be expressed as numbers with no common factors, or in their simplest form.

The Pythagorean theorem can be used to disprove this philosophy in finding the diagonal of a unit square.

 The diagonal's length can be found as the square is equal to the sum of the square of the two sides. Thus the square of the length of the diagonal is two, and thus the length is the square root of two. 

For a definitive proof against Pythagorean philosophy we must prove that the square root of two is irrational.

 The Irrationality of the Square Root of 2

If root 2 were rational we could express it as the ratio of two integers with no common factors. We will express it as a rational number and see what consequences it throws up.

 Re-arranging the ratio gives:

 Thus we can reason that the square of p is even, and thus p is even and can be expressed in the following way (where n is any positive integer)

 

Squaring p and substituting it into already known equations gives us:

 

 And thus:

So it can be said that the square of q is even, and also that q is even.

Thus, we have proven that the square root of two cannot be expressed as the ratio of two integers with no common factors and is therefore irrational.

QED

Thus we have proved how Pythagorean philosophy is incorrect as a naturally occuring number - the square root of 2 as the diagonal of a unit square - cannot be represented as the ratio of two integers with no common factors.