Pythagoras' Theorem
If we have a square with a tilted, smaller square inside (see diagram above), then we can come up with two expressions for the area of the larger square. The first squares the sum of lengths a and b; the second squares the length c, then adds the area of the smaller triangles surrounding the smaller, inner square.
Then we can solve these equations simulataneously for the square of c
Thus we have proved the sum of the squares of the two smallest sides in a right angled triangle is equal to the square of the hypotenuse
QED
The Square Root of 2
Pythagorean philsophy believed that everything in the universe could be expressed as the ratio of two integers. These ratios are known as rational numbers and can be also expressed as a non-recurring decimal. for example 10:5 is the same as 2.0. Also, these ratios must be expressed as numbers with no common factors, or in their simplest form.
The Pythagorean theorem can be used to disprove this philosophy in finding the diagonal of a unit square.
The diagonal's length can be found as the square is equal to the sum of the square of the two sides. Thus the square of the length of the diagonal is two, and thus the length is the square root of two.
For a definitive proof against Pythagorean philosophy we must prove that the square root of two is irrational.
The Irrationality of the Square Root of 2
If root 2 were rational we could express it as the ratio of two integers with no common factors. We will express it as a rational number and see what consequences it throws up.
Re-arranging the ratio gives:
Thus we can reason that the square of p is even, and thus p is even and can be expressed in the following way (where n is any positive integer)
Squaring p and substituting it into already known equations gives us:
And thus:
So it can be said that the square of q is even, and also that q is even.
Thus, we have proven that the square root of two cannot be expressed as the ratio of two integers with no common factors and is therefore irrational.
QED
Thus we have proved how Pythagorean philosophy is incorrect as a naturally occuring number - the square root of 2 as the diagonal of a unit square - cannot be represented as the ratio of two integers with no common factors.



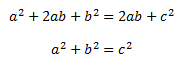

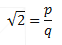

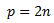


No comments:
Post a Comment