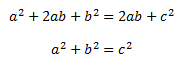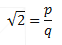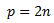Platonic Solids

Platonic Solids

This one is because I'm on a roll with geometry. (See escape velocity)

This post will prove that there are a limited number of regular three-dimensional solids and will determine the nature of these solids.

Euler said that a regular solid obeys the following rule (where V is the number of vertices, E is the number of edges, and F is the number of faces).

This can be expressed using E only by applying a little logic:

Every edge of a regular solid is shared by the sides of 2 adjacent polygons.

Every edge connects two vertices.

Therefore:

(where n is the number of sides each polygon has, and r is the number of polygons that meet at each vertex)

We can divide the new equation by 2E and rearrange to give:

n must be greater or equal to 3 as the simplest polygon is the triangle, and r must be greater than or equal to 3 as at least 3 vertices must meet in a polyhedron.

If both n and r were simultaneously greater than 3, the left hand side of the equation would be less than 2/3 and could not be satisfied if E is a positive integer (which it must be).

If n=3, the equation becomes:

This can give positive integer values of E for when r = 3, 4, and 5.

 If r=3, the equation becomes:

If n=3, we get E=6 again.

In both cases, n and r cannot be greater than or equal to 6. Because n and r must be between 3 and 6, and either n or r must be three for all solids, there is a limited number of valid combinations of n and r. There are only five of these combinations and thus there are only five regular solids.

We will now analyse these results to see what deescribes which solid. To describe the shape we wil use curly brackets to show {n, r}. From earlier we also know that: V=2E/r and F=2E/n, these will be used to determine the nature of these solids.

{3, 3}

When n=3 and r=3, then E=6. Thus V=4 and F=4. Thus we can deduce the following:
The solid consists of four regular triangles, three triangles meet at each of the four vertices forming six edges. This shape is therefore the tetrahedron.

{3, 4}

When n=3 and r=4, then E=12. Thus V=6 and F=8. Thus we can deduce the following:
The solid consists of eight regular triangles, four triangles meet at each of the six vertices forming twelve edges. This shape is therefore the octahedron.

{3, 5}

When n=3 and r=5, then E=20. Thus V=12 and F=20. Thus we can deduce the following:
The solid consists of twenty regular triangles, five triangles meet at each of the twelve vertices forming twenty edges. This shape is therefore the icosahedron.

{4, 3}

When n=4 and r=3, then E=12. Thus V=8 and F=6. Thus we can deduce the following:
The solid consists of four squares, three squares meet at each of the eight vertices forming twelve edges. This shape is therefore the cube.

{5, 3}

When n=5 and r=3, then E=30. Thus V=20 and F=12. Thus we can deduce the following:

The solid consists of twelve regular pentagons, three pentagons meet at each of the twenty vertices forming thirty edges. This shape is therefore the dodecahedron.

Thus, the tetrahedron, octahedron, icosahedron, cube, and the dodecahedron are the only five regular solids.

QED 

These solids were used in Kepler's first attempt at describing at describing a heliocentric model. It worked because the number of known planets at the time was five, and it seemed too much of a coincidence to Kepler. Unfortunately, it was; however, he still went on to discover his three laws of planetary motion.

Aristotle also believed that these solids corresponded to air, earth, fire, water. Apparantly, ordinary people were to be kept ignorant of the dodecahadron - which was not assosiated with an element. However, some philosophers at the time believed in an aether in which the planets moved, and some applied the starry appearance of the dodecahedron to the starry appearance of the night sky.

Escape Velocity

Earth's Escape Velocity

The escape velocity is the velocity required to send a body into orbit around another body, such as a planet. The escape velocity of Earth can be found by using geometry.

There is no escape...

To calculate the velocity, we need to know two numbers: the radius of the body you want to escape from, and the distance an escaping body will fall in one second. In the case of Earth, the radius is 6,380km and the distance fallen in one second in half of the figure for accelaration due to gravity, so we will call it g/2 for now.

Therefore we can say:

R = 6380000m

S = g/2

We can show the Earth as a two dimensional circle like this:

We can use a theorem of plane geometry to help us in our calculation. The tangient to a circle is the mena proportion between two parts of the diametre cut by an equal chord...

...and in algebra speak we get this which can be easily solved for x:

Remember: S = g/2

We can just plug in the values of the radius and for g (9.81ms^-2) to get 7900km if we are using 3 sig. fig.

Thus, as x is the distance we need to send our rocket ship in one second, we can divide by this one second to get a velocity. Thus:

For our friends in Europe.

For those using old money.

Thus, in order to escape the gravitational pull of the Earth and go into orbit, we will have to travel with a velocity close to 8 kilometres (5 miles) a second.

QED

Geometrical diagram made with Geogebra.

Pythagoras and Irrationality

Pythagoras' Theorem

If we have a square with a tilted, smaller square inside (see diagram above), then we can come up with two expressions for the area of the larger square. The first squares the sum of lengths a and b; the second squares the length c, then adds the area of the smaller triangles surrounding the smaller, inner square.

Then we can solve these equations simulataneously for the square of c

Thus we have proved the sum of the squares of the two smallest sides in a right angled triangle is equal to the square of the hypotenuse 

QED

The Square Root of 2 

Pythagorean philsophy believed that everything in the universe could be expressed as the ratio of two integers. These ratios are known as rational numbers and can be also expressed as a non-recurring decimal. for example 10:5 is the same as 2.0. Also, these ratios must be expressed as numbers with no common factors, or in their simplest form.

The Pythagorean theorem can be used to disprove this philosophy in finding the diagonal of a unit square.

 The diagonal's length can be found as the square is equal to the sum of the square of the two sides. Thus the square of the length of the diagonal is two, and thus the length is the square root of two. 

For a definitive proof against Pythagorean philosophy we must prove that the square root of two is irrational.

 The Irrationality of the Square Root of 2

If root 2 were rational we could express it as the ratio of two integers with no common factors. We will express it as a rational number and see what consequences it throws up.

 Re-arranging the ratio gives:

 Thus we can reason that the square of p is even, and thus p is even and can be expressed in the following way (where n is any positive integer)

 

Squaring p and substituting it into already known equations gives us:

 

 And thus:

So it can be said that the square of q is even, and also that q is even.

Thus, we have proven that the square root of two cannot be expressed as the ratio of two integers with no common factors and is therefore irrational.

QED

Thus we have proved how Pythagorean philosophy is incorrect as a naturally occuring number - the square root of 2 as the diagonal of a unit square - cannot be represented as the ratio of two integers with no common factors.